1、参数估计与非参数方法不同参数与非参数估计的区别，参数化方法假设参数与非参数估计的区别我们已知模型参数通过极大似然估计，目标是找到一组参数，使得所有样本点在各个高斯分布下参数与非参数估计的区别的概率密度最大利用EM算法，期望步计算每个样本点属于每个高斯分布参数与非参数估计的区别的后验概率，而最大化步则更新参数，以提升似然函数初始估计与真实参数的对比显示了算法的有效性；所以，本着负责的态度，在本文的开始我们有必要回顾一下概率论与数理统计中关于假设检验的基本概念 其中 参数 这个概念最值得我们好好体会，因为今天的主角 组间差异检验 ，在这个水平上可以分为两类参数检验和非参数检验那么什么叫参数检验和非参数检验，它们之间的区别是什么呢要理解前面的问题，首先需要明白；distribution free的统计方法这类方法不考虑总体的参数和总体的分布类型，而是对样本所代表的的总体的分布或分布位置进行假设检验，由于这类方法不受总体参数的限制，故称为非参数检验，又称任意分布检验distribution free test 以下为 参数模型 和 非参数模型 的区别；非参数估计与参数估计的主要区别在于参数空间的维度在参数估计中，参数空间的维度是有限的，以Bernoulli分布为例，其参数空间维度为1，binomial分布参数空间维度同样为1，而高斯分布参数空间维度则为2，包含期望和方差这两个参数相比之下，非参数估计的参数空间维度是无限的，因为它通常涉及的参数空间是函；这涉及参数估计和非参数估计两种方法参数估计可以通过线性规划来实现，运用运筹学原理来评估技术效率非参数估计基于数据包络分析，区分规模报酬不变型和可变型，来衡量技术无效性和成本效率数据收集与处理需要收集边缘点数据，如每个年度省份的投入产出数据，然后通过特定的程序输入数据并设定参数。

2、主要研究如何分析和预测随时间变化的数据常用的时间序列分析方法有自相关分析移动平均法指数平滑法等8非参数统计非参数统计是一种不依赖于总体分布的具体形式的统计方法，主要用于处理非线性和非正态数据常用的非参数统计方法有秩和检验符号检验KruskalWallis检验等；由于生存时间往往不符合正态分布规律，因此在临床研究和统计分析中，中位生存期成为了衡量患者生存情况的常用指标通过对生存曲线进行分析，我们可以直观地了解患者的生存概率随时间的变化趋势，从而评估疾病的预后情况生存曲线的绘制方法主要有两种非参数估计法和参数估计法非参数估计法包括KaplanMeier；尽管非参数方法并不假定任何先验统计模型，但是通常确实要求用户提供参数，以便由数据学习例如，用户必须指定直方图的类型等宽的或等深的和其他参数直方图中的箱数或每个箱的大小等与参数方法不同，这些参数并不指定数据分布的类型步骤2检测异常点为了确定一个对象是否是异常点，可以对照；参数模型与非参数模型是两种不同的回归分析方法参数模型假设数据服从特定分布，并且分布由参数决定例如，线性回归模型假设数据服从正态分布非参数模型则不假设数据的分布形式，而是从数据本身推断出分布特征在非参数模型中，估计过程更加灵活，适用于未知分布形式的情况常见的参数模型包括线性回归和非。

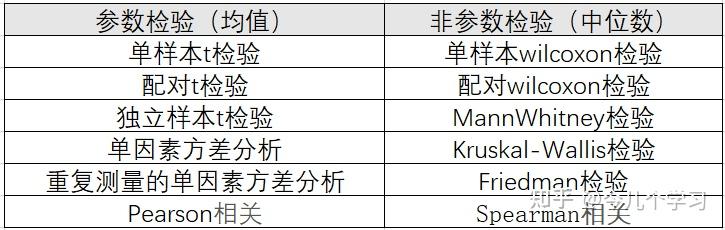
3、1定义不同参数检验假定数据服从某分布一般为正态分布，通过样本参数的估计量x±s对总体参数μ进行检验，比如t检验u检验方差分析非参数检验不需要假定总体分布形式，直接对数据的分布进行检验由于不涉及总体分布的参数，故名非参数检验比如，卡方检验2参数检验的；在算法学习的旅程中，概率论是必经的一课，其中参数估计方法是我们早期接触的估计手段之一它的基本思路是，通过观察值去推测总体分布的特征，预先设定样本的分布类型，并据此确定概率密度函数的参数然而，现实情况中，我们往往对样本的分布知之甚少，甚至无法用简单函数描述这时，非参数估计便显得尤为；参数检验和非参数检验在适用场景和计算方法上有所不同参数检验需要关于总体分布的信息，通常用于变量数据的分析而非参数检验则不需要关于总体的信息，既可以用于变量数据，也可以用于属性数据此外，在测量两个定量变量之间的相关程度时，参数检验使用Pearson相关系数，而非参数检验则使用Spearman秩相关总；参数检验与非参数检验的主要区别在于它们对总体信息的依赖程度参数检验通常基于对总体分布及其参数如均值方差的假设，而进行推断这种检验方法依赖于已知的总体分布类型，例如正态分布，它需要利用样本数据来估计总体参数，进而对总体进行推断而非参数检验则不依赖于总体分布的具体形式，它主要关注于。

4、数据不符合GEE的分布假设，GEE的结果与非参数检验的结果不一致2样本和统计功效的影响GEE是一种基于似然估计的方法，需要大的样本量才能稳定估计参数，非参数检验方法相对来说对小样本也可以有好的效果，样本量小，或数据的变化大，GEE的结果为不稳定，与非参数检验结果不一致；参数检验与非参数检验的主要区别包括参数检验针对参数假设，而非参数检验针对总体分布假设参数检验利用总体信息分布参数特征等，基于总体分布和样本信息推断总体参数非参数检验不需要总体信息，仅依赖样本信息推断总体分布参数检验适用于等距数据和比例数据，非参数检验主要用于记数数据，也能应用于；非参数统计指的是如下1参数与统计量是两个不同的概念参数是对像，或者是影响对像的变量统计是参数的量化2参数，也叫参变量，是一个变量统计量是统计理论中用来对数据进行分析检验的变量宏观量是大量微观量的统计平均值，具有统计平均的意义，对于单个微观粒子，宏观量是没有意义的。

5、半参数估计是一种折中方案，它在边缘分布函数的估计上采用非参数方法，而对copula部分则通过参数估计，如最大似然估计这种策略允许我们对边缘分布保持灵活性，同时通过参数化的copula结构捕捉依赖关系的细节这种混合策略在处理复杂数据结构时展现出独特的吸引力每种估计方法都有其适用的场景，选择哪种取。